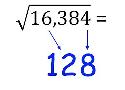578 liens privés
Wow ! Excellente technique.
C'est un exercice de calcul pour lequel je n'avais pas d'astuce.
Là ça passe par quelques étapes simples :
- Connaître le carré des chiffres de 0 à 9.
- Se rendre compte de l'effet miroir de l'unité autour du carré de 5.
- Utiliser cela pour apprécier le carré de l'unité+dizaine de notre devinette (A).
- Idem pour la centaine+millier (B).
- Si besoin de discriminer, on fait le carré de
(B)|5qui s'estime avec(B) × (B)+1|5.
(bon, faut voir la vidéo en vrai pour bien comprendre quand même)
Ah oui, c'est le fameux principe qui permet avec noir et blanc de générer plusieurs tons de couleurs. Il y a plusieurs algorithme.
En français, ça s'appelle la « diffusion d'erreur ». Je ne sais pas si ça porte bien son nom…
Aaaah la sérendipité… Je cherchais des informations sur le phénomènes liés aux "aliments mucogènes" et je tombe sur diverses façons de calculer avec les mains :
- La plus commune (pour "nous" du moins) : un doigt levé = 1 unité. On peut compter de 0 à 10 avec 2 mains.
- J'avais découvert une technique où avec le pouce on vient toucher une phalange de chaque doigt ; 3 phalanges par doigt (hors pouce) × 4 doigts = 12 unité avec 1 main. On peut compter de 0 à 12×12=144 avec 2 mains.
- Là je découvre le Chinese number gestures. On peut compter de 0 à 10 avec une seule main en levant les doigts : 1 avec index (I) ; 2 avec I+Majeur (M) ; 3 = I+M+Annulaire (R) ; 4 = I+M+R+Auriculaire (A) ; 5 = Pouce (P) + IMRA ; 6 = P---A ; 7 = PI--- ; 8 = PIM-- ; 9 = PIMR- ; 10 = poing fermé, aucun doigt levé. On peut donc compter de 1 à 100 avec 2 mains.
- Le Finger binary : évidemment, on calcule en binaire. On a donc 2^5=32 unités par main ; on peut donc aller de 0 à 2^10=1024.
- Et là le Chinsanbop qui permet, à la manière d'un boulier, de calculer de 0 à 99.
J'adore !
Cela me fait penser à la technique pour les tables de multiplications (pour des paires de chiffres entre 5 et 10 inclus) à la main et qui est infaillible.
En fait l'article suivant de Wikipédia en français résume bien les choses aussi : https://fr.wikipedia.org/wiki/Dactylonomie :-)
Wow, ça doit faire… au moins 5 ans que je cherche régulièrement le nom de cette loi mathématique.
« Quand on étudie un ensemble de données numériques, on pourrait s'attendre à voir les chiffres de 1 à 9 apparaître à peu près aussi fréquemment comme premier chiffre d'un nombre, soit avec une fréquence de 11,1% = 1/9 pour chacun. Or, contrairement à cette intuition (biais d'équiprobabilité), pour près du tiers des observations, le 1er chiffre significatif le plus fréquent est 1. Le chiffre 2 est ensuite lui-même plus fréquent que le 3… et la probabilité d'avoir un 9 comme premier chiffre significatif n'est que de 4,6 % . C'est une loi observée aussi bien dans les mathématiques sociales, c'est-à-dire les sciences humaines et sociales, que dans des tables de valeurs numériques comme celles qu'on rencontre en physique, en BTP, en économie (taux de change), ou même dans les numéros de rue de son carnet d'adresses. »
Cela signifie que pour vérifier (empiriquement !) la vraisemblance d'un ensemble de données, il suffit de regarder la répartition des chiffres : si vous avez plus de 8 et 9 que de 1 et 2, c'est peut-être que les données ont été manipulées ou biaisées.
Édition 2020-04-30T12:05 : à compléter avec le test du Khi²
1/φ=φ-1
!!!
(soit ≈0.61803398875)
Très sympa cette idée, est très amusante.
Le seul problème c'est quand je lis ceci : "Georg, you're the father of the set theory, I need you for a proof." En bref : « j'ai besoin de toi pour prouver une théorie »...
Ce n'est pas possible de prouver une théorie puisque, comme son nom l'indique, ce n'est qu'une théorie. cf https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_des_quatre_couleurs
(bon, Timo relèverait qu'il y a une nuance entre théorème et théorie, mais bon...)